Determining Charateristics of Progenitor¶

Introduction¶

The scenario this code attempts to address is the following. Say you observed a binary system in a galaxy that was a certain off-set from the center of that galaxy. You also have information about the masses of the system you observed. What, if anything, can you say about some of the properities of the system at its initial creation in the galaxy. Specifically, at the creation of the larger component mass of the system via a Supernova. The properities of the system at this stage that one needs to sample over inclue such as pre-supernova semi major axis, supernova kick, Mass of pre-supernova helium star, etc.

In order to accomplish this, one would need to load in properities of the galaxy in which this system was created. For example this includes information such as:

'Mspiral' # mass of the spiral (Msun) # NOTE: this information is not available, for now set to 0
'Mbulge' # Mstellar from 2MASS (Msun)
'Mhalo'  # Mhalo from 2MASS (Msun)
'D1':    # major axis from 2MASS (arcmin)
'D2':    # minor axis from 2MASS (arcmin)

>>> Galaxy = constr_dict.galaxy(galaxy_name, samples, r_eff, offset, h)

This is done using galaxy(). In addition to creating a dictionary of galaxy properities, we must assume a Galaxy model for this galaxy. The current model that is implemented and works is Hernquist Hernquist_NFW().:

>>> gal=Hernquist_NFW(Galaxy['Mspiral'], Galaxy['Mbulge'], Galaxy['Mhalo'], Galaxy['R_eff'], h, rcut=100)

Once, the galaxy and galaxy model is selected it is now time to sample over a large set of initial conditions of the system that you observed. These initial conditions include, the mass of pre supernova helium star, the kick velocity of the supernova, the pre supernova semi major axis, initial distance from center of galaxy. After creating these intiail conditions we evolve the system to see if a.) there is a merger within some reasonable time (<14 Giga years) and b.) it merged at the appropriate off-set (with some error) from the center of the galaxy. The only value sampled over in the following section that is not relevant to the initial conditions of the system that you observed is the distance uncertianity of the hose galaxy (which impacts the uncertainity in the observed off set). This value is not necessary as fixed inflated errors bars can be used in order to be “safe”. In the following sections, we dive into the code used to accomplish this.

Sampling Initial Conditions¶

In the executable, all of the sampling is done as such:

Nsys=args.trials
dEfrac = 0.0

# Initialize random draws for some parameters based on number of trials
print "\nSampling binary parameters..."

Mcomp_dist, Mns_dist = samp.sample_masses(samples, method=args.Ms, size=Nsys)
# (Msun)

d_dist = samp.sample_distance(samples, method=args.distance, size=Nsys)
# (Mpc) (Not necessarily used, as inflated error bars in the observed galactic offset can be used to account for the distance (or uncertianity in distance) of the galaxy


Apre_dist = samp.sample_Apre(Amin=0.1, Amax=10.0, method=args.Apre, size=Nsys)
# (Rsun)

epre_dist = samp.sample_epre(method=args.epre, size=Nsys)
# (dimensionless)

PDFR = samp.initialize_R()

R_dist = samp.sample_R(PDFR, Nsys)
# (kpc)

PDFMhe = samp.initialize_Mhe(0.6)
ECSPDFMhe = samp.initialize_Mhe(0.1)
CCSPDFMhe = samp.initialize_Mhe(1.0)
dumrand = np.random.uniform(0,1,size=Nsys)
Mhe_dist = samp.sample_Mhe(Mmin=Mns_dist, method=args.Mhe, size=Nsys, PDF=PDFMhe, ECSPDF=ECSPDFMhe, CCSPDF=CCSPDFMhe, irand=dumrand)
# (Msun)
ECS,CCS = samp.initialize_Vkick()

Vkick_dist = samp.sample_Vkick(method=args.Vkick, size=Nsys, ECSPDF=ECS, CCSPDF=CCS, Mhe=Mhe_dist, irand=dumrand)

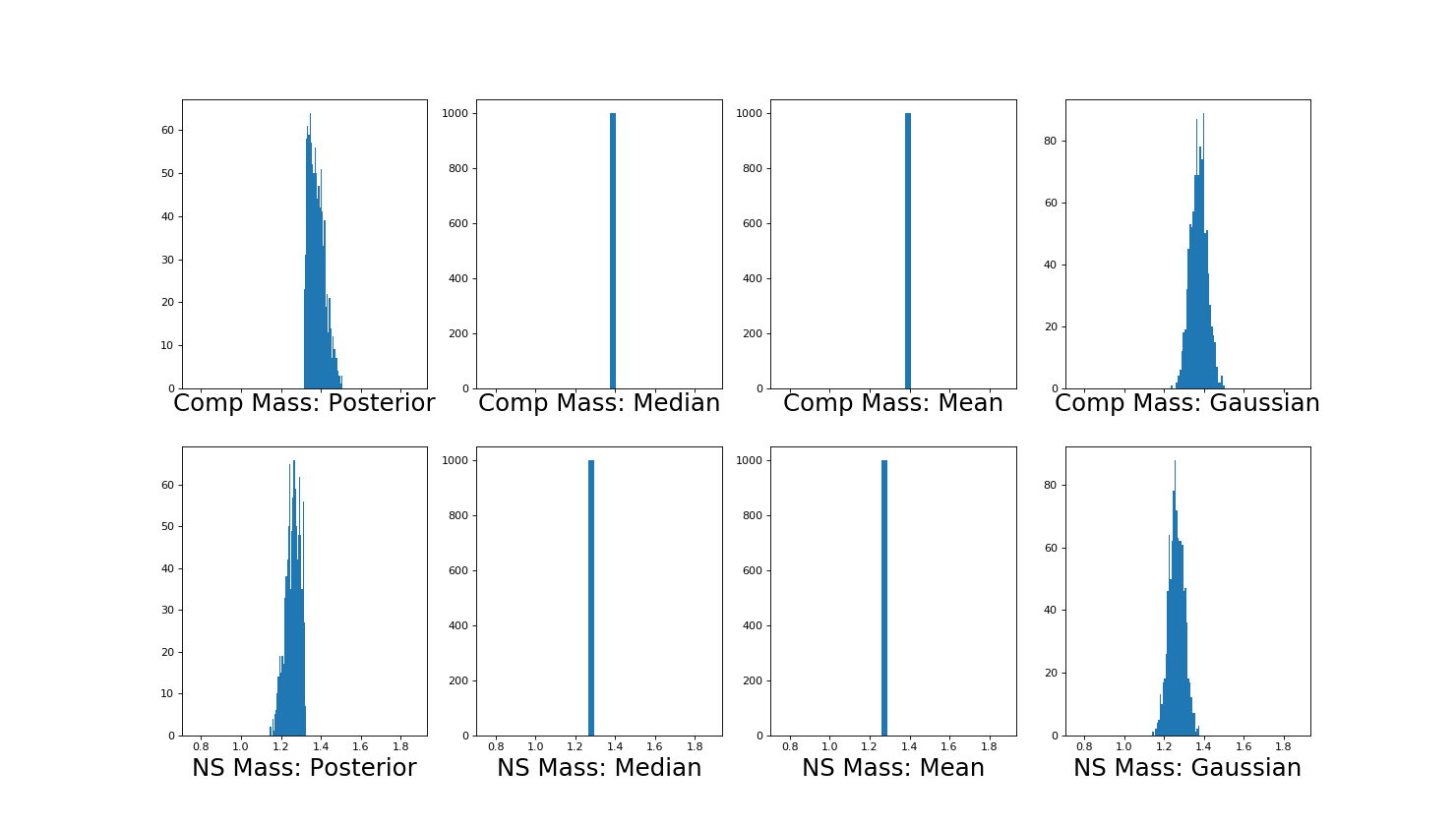
Component and Secondary Mass¶

sample_masses()

The available methods for sampling are ‘gaussian’, ‘mean’, ‘median’, or ‘posterior’:

The posterior method is used by default. This simply means that we draw samples directly from Gravitational Wave parameter estimation pdf of the source frame masses of the observed binary system:

>>> Mcomp_dist, Mns_dist = samp.sample_masses(samples, method=args.Ms, size=Nsys)

(Source code, png, hires.png, pdf)

Distance¶

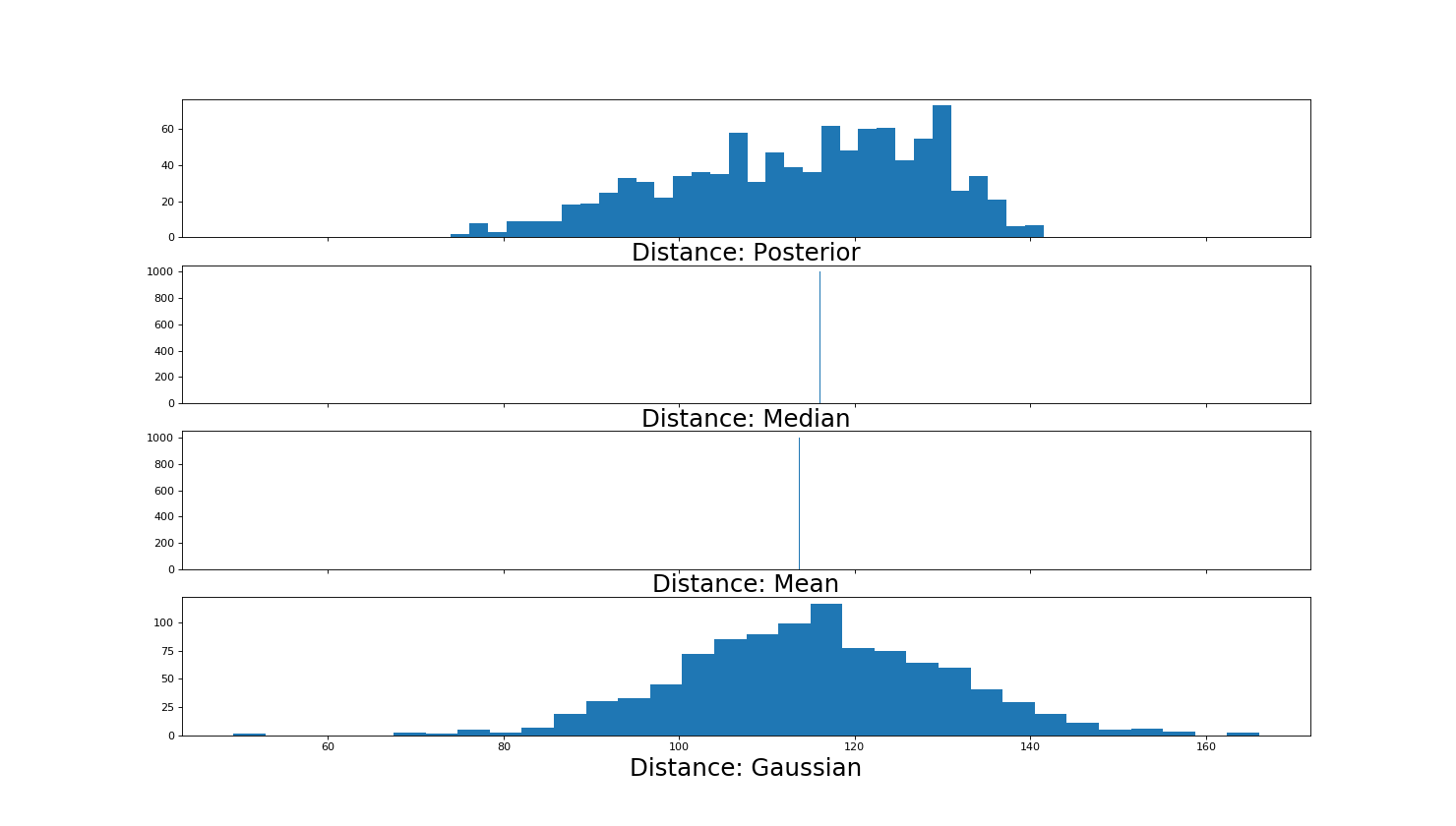
sample_distance()

The default method is median (i.e. the median value from the Gravitational Wave parameter estimation pdf of distance. Again, this value is critical in calculating the uncertainity in the observed offset and can be circumvented by smartly chosen inflated error bars in the observed of set:

>>> d_dist = samp.sample_distance(samples, method=args.distance, size=Nsys) # (Mpc)

(Source code, png, hires.png, pdf)

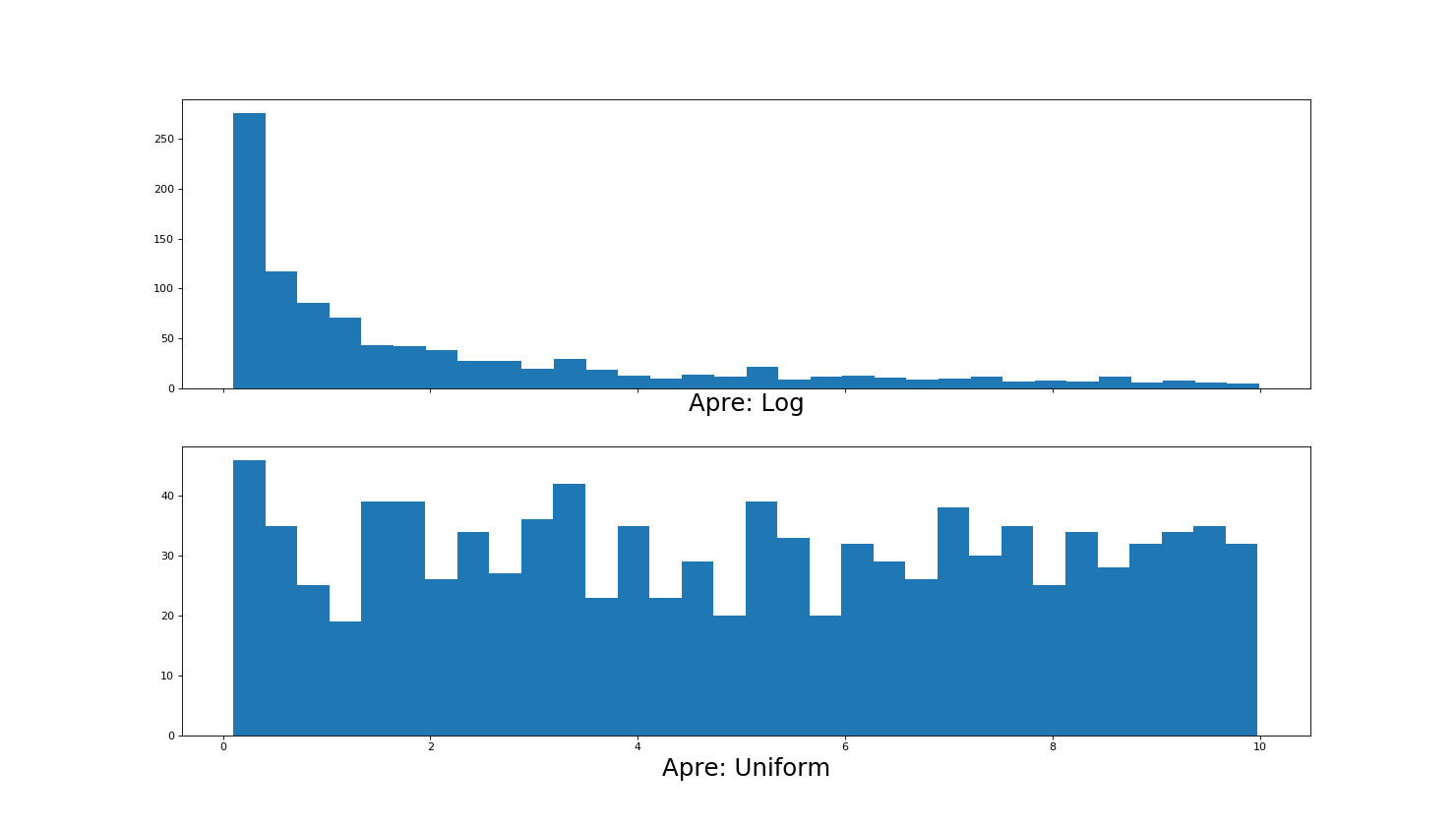
Pre Supernova Semi Major Axis¶

sample_Apre()

The available methods for sampling are ‘uniform’ and ‘log’. This value is the pre-supernova semi major axis.:

>>> Apre_dist = samp.sample_Apre(Amin=0.1, Amax=10.0, method='uniform', size=Nsys)

(Source code, png, hires.png, pdf)

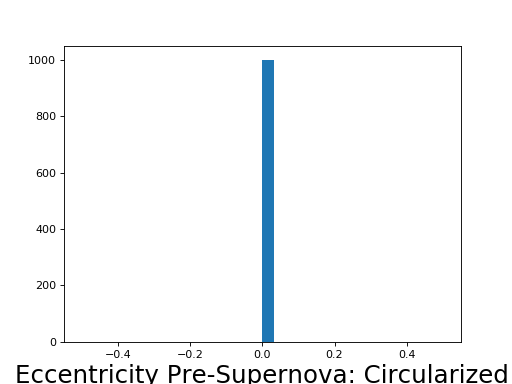
Pre Supernova eccentricity¶

Because we assume circular orbits, we assume that the eccentricity of the system pre second supernova is neglible (set to 0 here), but do account for effects of eccentricity post second supernova. sample_epre()

The available method for sampling is ‘circularized’:

>>> epre_dist = samp.sample_epre(method='circularized', size=Nsys)

(Source code, png, hires.png, pdf)

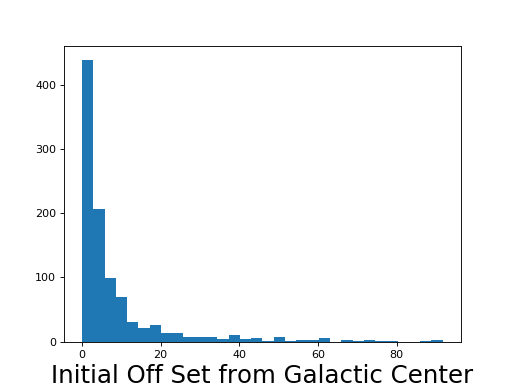
Initialize Off Set From Galactic Center¶

We create a custom distribution to sample the intiial galactic offset of the pre second supernova system. The r_eff is used to control sampling at galactic offsets that are unrealistically far away from the center of the galaxy (i.e. we expect less binaries to form super far away from the galactic center and moreover some initial offsets may in fact be outside the plausible “diameter” of the galaxy. To initialize this PDF, we use initialize_R(), to sample some number of outcomes from this PDF we use sample_R():

>>> PDFR = samp.initialize_R()
>>> R_dist = samp.sample_R(PDFR, Nsys) # (kpc)

(Source code, png, hires.png, pdf)

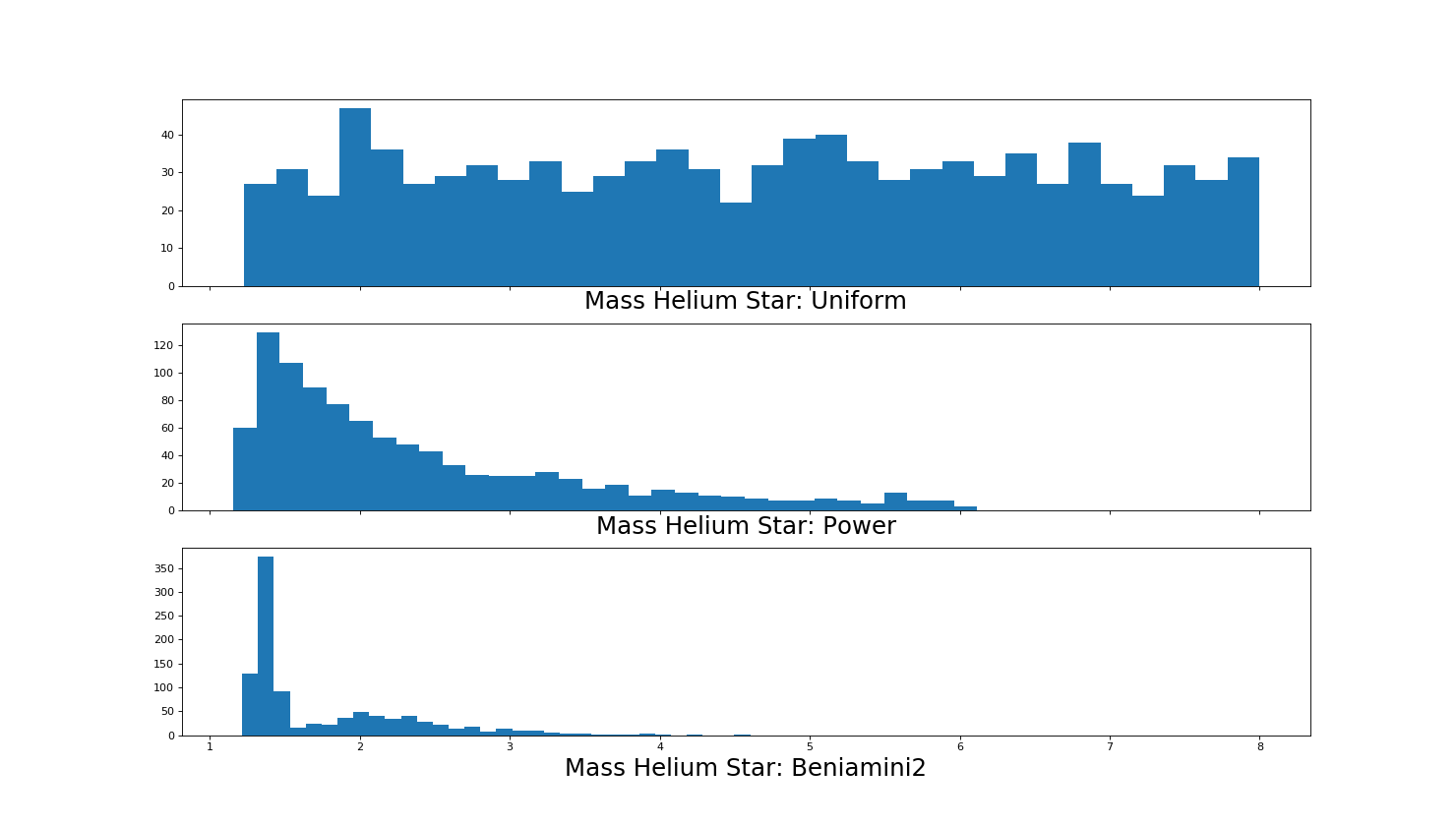
Mass of Pre Supernova Helium Star¶

initialize_Mhe() sample_Mhe():

Available methods include ‘power’, ‘uniform’, ‘beniamini2’.

Beniamini2 draws from two distributions, low eccentricity (ECS) and high eccentricity (CCSN), for the pre-supernova Helium Star and Kick Velocity distributions. It does so in a 60 40 split which is motivated by the number of such systems we observe in the Milky Way (6 and 4) which is shown in Figure 2. The initialized values for the distribution are motivated form the paper where the deltaM_0 and Vkick_0 for ECS that corresponded to the maximum likelihood weere 0.1 and 5.0, respectively, and the deltaM_0 and Vkick_0 for ECS that corresponded to the maximum likelihood for CCSN were 1.0 and 158.0 respectively.:

>>> ECSPDFMhe = samp.initialize_Mhe(0.1)
>>> CCSPDFMhe = samp.initialize_Mhe(1.0)
>>> dumrand = np.random.uniform(0,1,size=Nsys)
>>> Mhe_dist = samp.sample_Mhe(Mmin=Mns_dist, method='uniform', size=Nsys, PDF=None, ECSPDF=ECSPDFMhe, CCSPDF=CCSPDFMhe, irand=dumrand) # (Msun)

(Source code, png, hires.png, pdf)

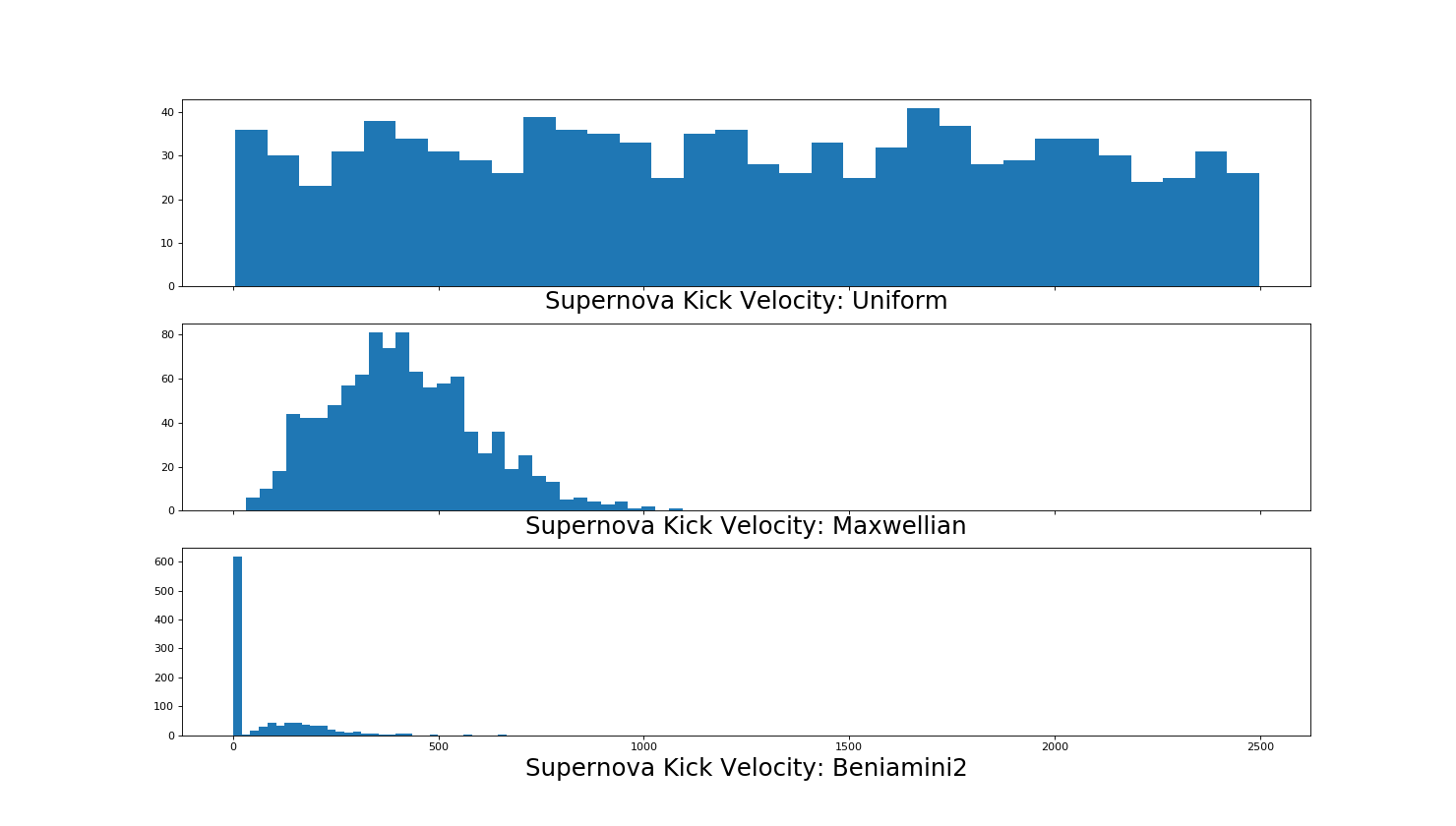
Supernova Kick Velocity¶

initialize_Vkick() sample_Vkick()

Available methods include ‘maxwellian’, ‘uniform’, ‘beniamini2’.

Beniamini2 draws from two distributions, low eccentricity (ECS) and high eccentricity (CCSN), for the pre-supernova Helium Star and Kick Velocity distributions. It does so in a 60 40 split which is motivated by the number of such systems we observe in the Milky Way (6 and 4) which is shown in Figure 2. The initialized values for the distribution are motivated form the paper where the deltaM_0 and Vkick_0 for ECS that corresponded to the maximum likelihood weere 0.1 and 5.0, respectively, and the deltaM_0 and Vkick_0 for ECS that corresponded to the maximum likelihood for CCSN were 1.0 and 158.0 respectively.:

>>> ECS,CCS = samp.initialize_Vkick()
>>> Vkick_dist = samp.sample_Vkick(method=args.Vkick, size=Nsys, ECSPDF=ECS, CCSPDF=CCS, Mhe=None, irand=dumrand)

(Source code, png, hires.png, pdf)

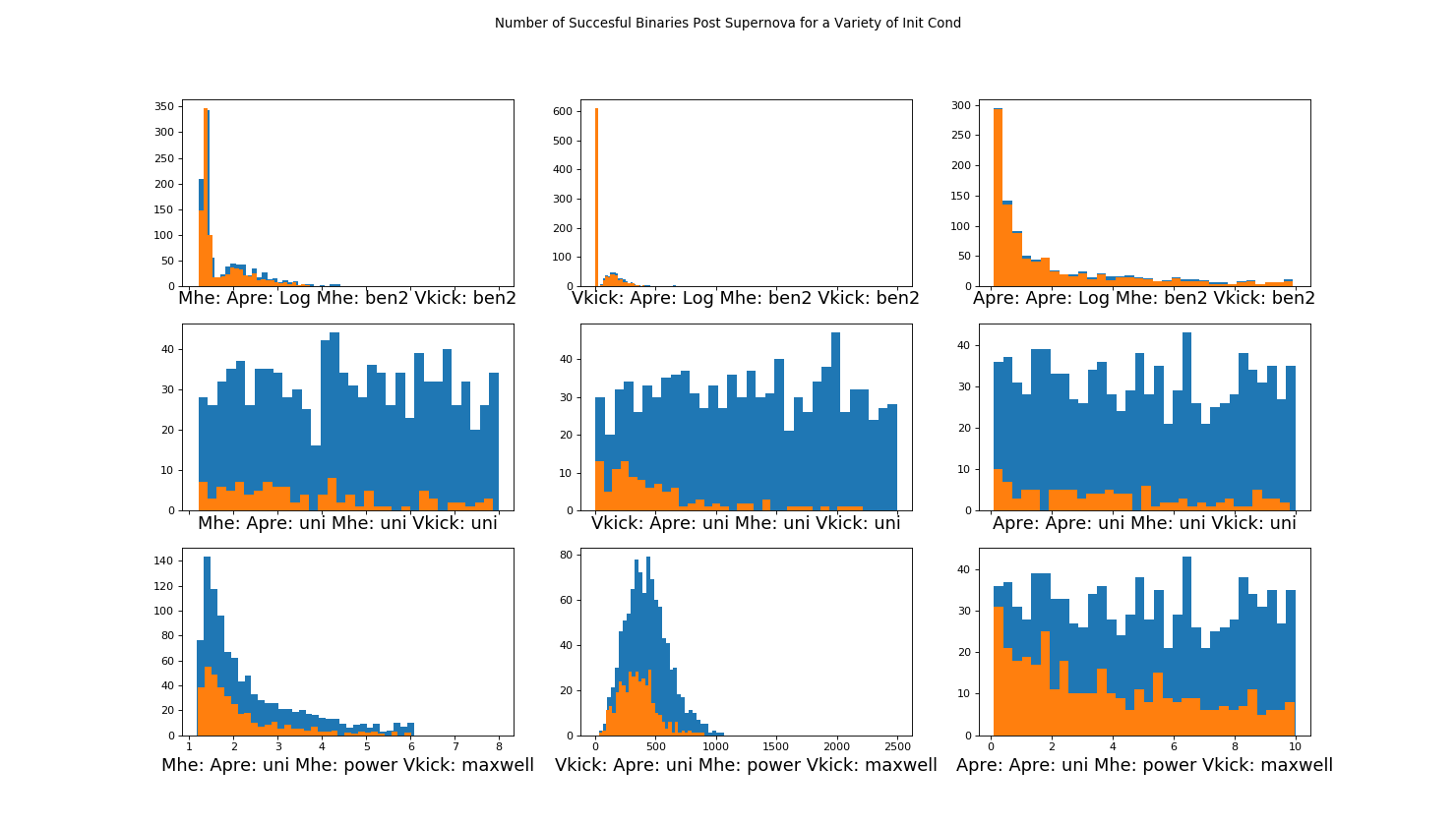
Creating and Evolving the System¶

Now that we have successfully sampled a number of initial conditions for our pre-Supernova binary, we can create the System:

>>> # initialize System class with pertinent parameters
>>> T=System(gal, R, Mns, Mcomp, Mhe, Apre, epre, d, Vkick, sys_flag=args.sys_flag)

In the following sub-sections we discuss the forward modelling that occurs after the creation of this system.

Supernova¶

The very first thing that you have to do is take the initial conditions of your pre-Supernova Helium star + neutron star system, and evolve Helium star through supernova to the post supernova object + neutron star system. Naturally, not all initial conditions of pre-supernova helium star semi-major axis, etc. will successfully result in the creation of a binary system. Therefore, the first check of the forward modeling occurs, that is, does a successful binary result from the supernova.

System Resulting from Supernova of Helium Star¶

SN()

We utilize Kalogera 1996 in order to determine the properities of the post supernova binary (such as eccentricity of the system post supernova, additional mass etc.) From the documnetation, We use Eq 1, 3, 4, and 34: giving Vr, Apost, epost, and (Vsx,Vsy,Vsz), respectively. Also see Fig 1 in that paper for coordinate system. After calculating this post super system values we check for whether this system would be expected to result in the successful creation of a binary. We check 4 separate equations detailed in Willems et al 2002. Specifically, we use eq 21, 22, 23, 24, 25, 26 for checks of SN survival:

>>> T.SN()

(Source code, png, hires.png, pdf)

Evolving System Through Galaxy¶

In order to forward model successfully created binaries through the galaxy, one must calculate first how long it will take for the merger of the system in order to set the upper bound on the ODE used to evolve the Velocity (and X,Y,Z coordinates) of the system through the galaxy.

Time to Merger Peters 1964¶

setTmerge() Checked against Peters 1964:

>>> # set merger time for trajectory integration, specify Tmin and Tmax in Gyr
>>> T.setTmerge(Tmin=0.0, Tmax=14.0)

Distance of Binary From Center¶

First, you randomly select from initial XYZ direction. setXYZ_0() Next, you randomly select an initial velocity direction setVxyz_0(): Then based on Tmerge you solve an ODE and evolve XYZ until merger. doMotion():

>>> # choose random location on sphere of radius R
>>> T.setXYZ_0()
>>> # choose random direction for circular velocity, and add SN-imparted velocity to get V0
>>> T.setVxyz_0()

>>> # integrate trajectory until Tmerge
>>> T.doMotion()

Check that conservation of energy is obeyed¶

energy_check() Calculate the initial Energy of the system and the final energy and make sure it is conserved to within some small error (0.001):

>>> # check for energy conservation, and hold onto highest offset
>>> T.energy_check()
>>> if T.dEfrac > dEfrac:
>>>     dEfrac = T.dEfrac

Checking Offset¶

Finally, You have a location for where in the galaxy your system merged. It is in XYZ so project onto XY plane and check if it matches to the observed off set (with some uncertainty in that offset accounted for). check_success()

Exploring Seemingly Optimal SN Kick Velocities¶

Two special case runs include setting –system-flag = ‘tangential’ or –system-flag = ‘radial_simple’.

These special realizations of the code ask the following questions: “Let us imagine the most seemingly optimal kick velocity direction of the SN that would result in getting us from some initial galactic offset that is smaller than the observed offset to the observed offset. This is the “radial_simple” case and it means that all of the kick velocity is “straight out” in the x direction. Conversely, let us imagine the most seemingly unoptimal way to get from some initial galactic offset that is smaller than the observed offset to the observed offset. This is the tangential case, which means all of velocity is perpendicular to the orbit.” How would one explore the results from such systems?

We simply do a special toy sampling in kick velocity (uniform 0 to 1000), and initial offset from center of the galaxy (uniform from 0.001 to observed offset). [Code](https://github.com/astro-traj/astro-traj/blob/master/bin/LIGOTraj#L151):

if args.sys_flag=='radial_simple' or args.sys_flag=='tangential' or args.sys_flag=='radial_simple2' or args.sys_flag=='tangential2':

    R_dist = np.linspace(0.001,Galaxy['offset'],10)
    Vkick_dist=np.linspace(0,1000,100)
    RV=np.array([[rr,vv] for rr in R_dist for vv in Vkick_dist]).transpose()
    R_dist=RV[0]
    Vkick_dist=RV[1]

In addition, we check this toy sampling for a discrete set of realization of Mhs, Mhe, Mcomp and Apre. [Code](https://github.com/astro-traj/astro-traj/blob/master/bin/LIGOTraj#L168):

if args.sys_flag=='tangential' or args.sys_flag=='radial_simple':
    Mns = 1.097
    Mcomp = 1.713
    Mhe = 4.5
    Apre = 2.0

Assuming these types of kick directions will impact what initial Vsys, X0, Y0, Z0, ad Vx0, Vy0, and vz0 are calculated/assumed. For radial X0, is initial offset and vX0 is Vsys with Vy0 = vz0 = Y0 = z0 = 0. [Code](https://github.com/astro-traj/astro-traj/blob/master/bin/LIGOTraj#L202):

if T.sys_flag=='radial_simple' or T.sys_flag=='radial_simple2':
    if R>Galaxy['offset']:continue
    T.SN()
    T.flag=9
    T.X0,T.Y0,T.Z0=T.R,0.,0.
    T.Vx0,T.Vy0,T.Vz0 = T.V_sys,0.,0.
    T.Tmerge = 0.1*u.Gyr.to(u.s)
    T.doMotion()

For tangential, X.Y.Z and Vz,Vy,Vz are calculated as normal [Code](https://github.com/astro-traj/astro-traj/blob/master/bin/LIGOTraj#L182):

if T.sys_flag=='tangential' or T.sys_flag=='tangential2':
    if R>Galaxy['offset']:continue
    T.SN()
    T.setXYZ_0()
    T.setVxyz_0()
    T.flag=9
    T.Tmerge = 0.1*u.Gyr.to(u.s)
    T.doMotion()

but Vsys is [Code](https://github.com/astro-traj/astro-traj/blob/master/astro_traj/system.py#L299):

#Rotate by omega while keeping perpendicular to R
Vp_rot = (Vp*np.cos(omega)) + (np.cross(k,Vp)*np.sin(omega))
Vp_rot_tot = np.sqrt((Vp[0]**2)+(Vp[1]**2)+(Vp[2]**2))
if self.sys_flag == 'tangential' or self.sys_flag== 'tangential2':
    vsys = [V_sys*Vp_rot[0]/Vp_rot_tot,V_sys*Vp_rot[1]/Vp_rot_tot,V_sys*Vp_rot[2]/Vp_rot_tot]

And in the SN kick calculated here the kick vector is set as follows:

[Code](https://github.com/astro-traj/astro-traj/blob/master/astro_traj/system.py#L129):

if self.sys_flag == 'radial_simple' or self.sys_flag == 'tangential' or self.sys_flag == 'radial_simple2' or self.sys_flag == 'tangential2':
    Vkx,Vky,Vkz=0,-Vkick,0

Backward Modeling¶

Backward modeling would be to say let us strt with a system of known quanity (i.e. observed offset and some T merge) and see if we can work backwards and retrieve our initial conditions. The assumptions made in the type of systems and the modeling of the velocity of the binary (F=ma), are simple enough that checks in the forward modeling such as conservation of energy are enough to ensure the sanity of the code.